Hierarchical Process Reward Models are Symbolic Vision Learners

Shan Zhang^1,5,*,†, Aotian Chen^2,*, Kai Zou³, Jindong Gu⁴, Yuan Xue^2,‡, Anton van den Hengel¹

¹Adelaide AIML ²Ohio State University ³NetMind.ai ⁴University of Oxford ⁵Data61 & CSIRO

^*Core Contribution ^†Project Lead ^‡Corresponding Author

Comparison of latent spaces formed by semantic auto-encoder and symbolic auto-encoder. Semantic auto-encoders capture color and texture, which are uninformative for semantically sparse diagrams. Our symbolic auto-encoder forms structured latent spaces representing dependencies among primitives, with the decoder reconstructing diagrams based on visual-logic rules.

Abstract

Symbolic computer vision represents diagrams through explicit logical rules and structured representations, enabling interpretable understanding in machine vision. This requires fundamentally different learning paradigms from pixel-based visual models. Symbolic visual learners parse diagrams into geometric primitives—points, lines, and shapes—whereas pixel-based learners operate on textures and colors. We propose a novel self-supervised symbolic auto-encoder that encodes diagrams into structured primitives and their interrelationships within the latent space, and decodes them through our executable engine to reconstruct the input diagrams. Central to this architecture is SymHPR (Symbolic Hierarchical Process Reward Modeling), which applies hierarchical step-level parsing rewards to enforce point-on-line, line-on-shape, and shape-on-relation consistency.

Evaluations across reconstruction, perception, and reasoning tasks demonstrate the effectiveness of our approach: achieving a 98.2% reduction in MSE for geometric diagram reconstruction, surpassing GPT-4o by 0.6% with a 7B model on chart reconstruction, improving by +13% on the MathGlance perception benchmark, and by +3% on MathVerse and GeoQA reasoning benchmarks.

Method

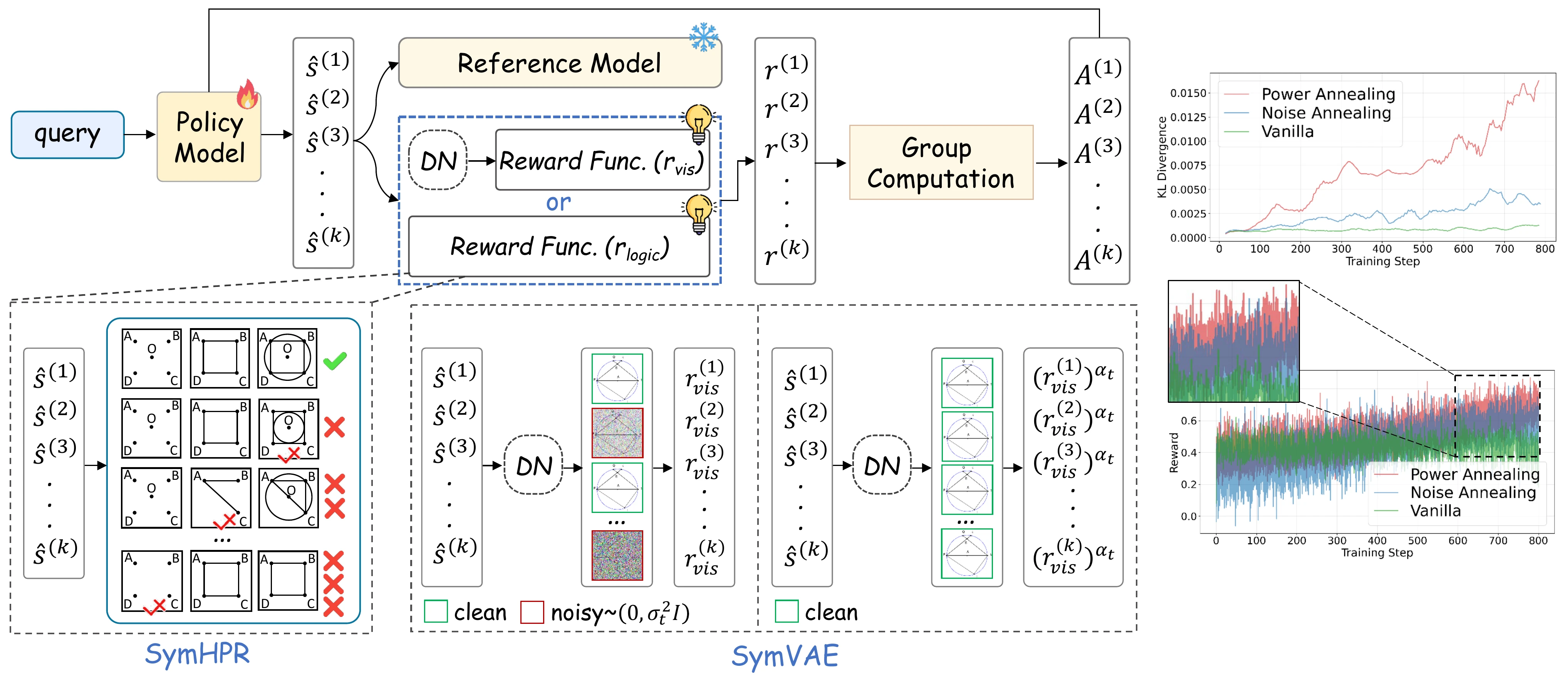
Key Innovations

Cost-Free Dataset Construction: A synthetic logic-form engine that constructs structured parsing paths (Point → Line → Shape → Shape Properties → Geometric Relations) paired with rendered diagrams, eliminating manual annotation.
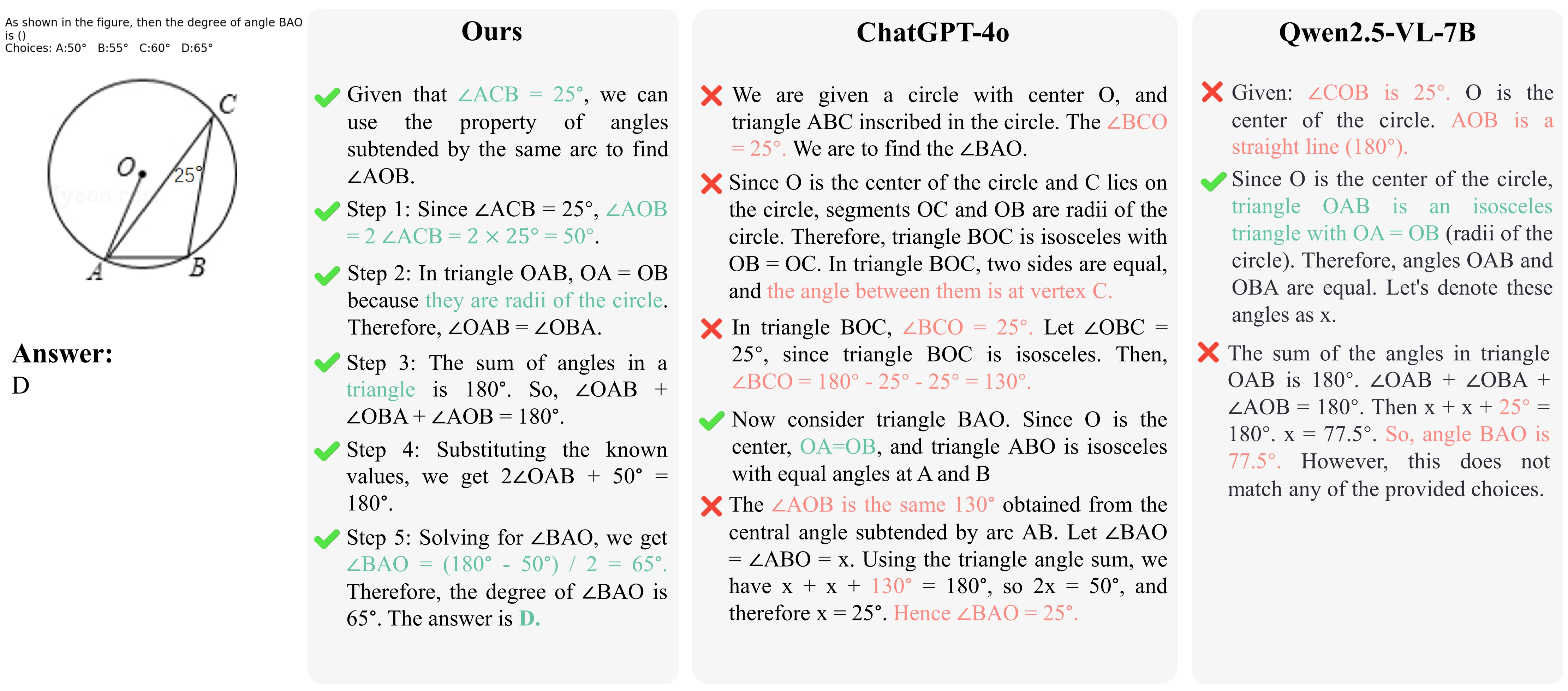
Rule-based Rewards: Computed via verifiable metrics such as F1 scores and L2 distances, removing hallucinated supervision.
Hierarchical Dependency Modeling: Enforces step-level constraints (point-on-line, line-on-shape, shape-on-relation), ensuring geometric rewards are granted only when lower-level detections are reliable.

Symbolic Auto-Encoder

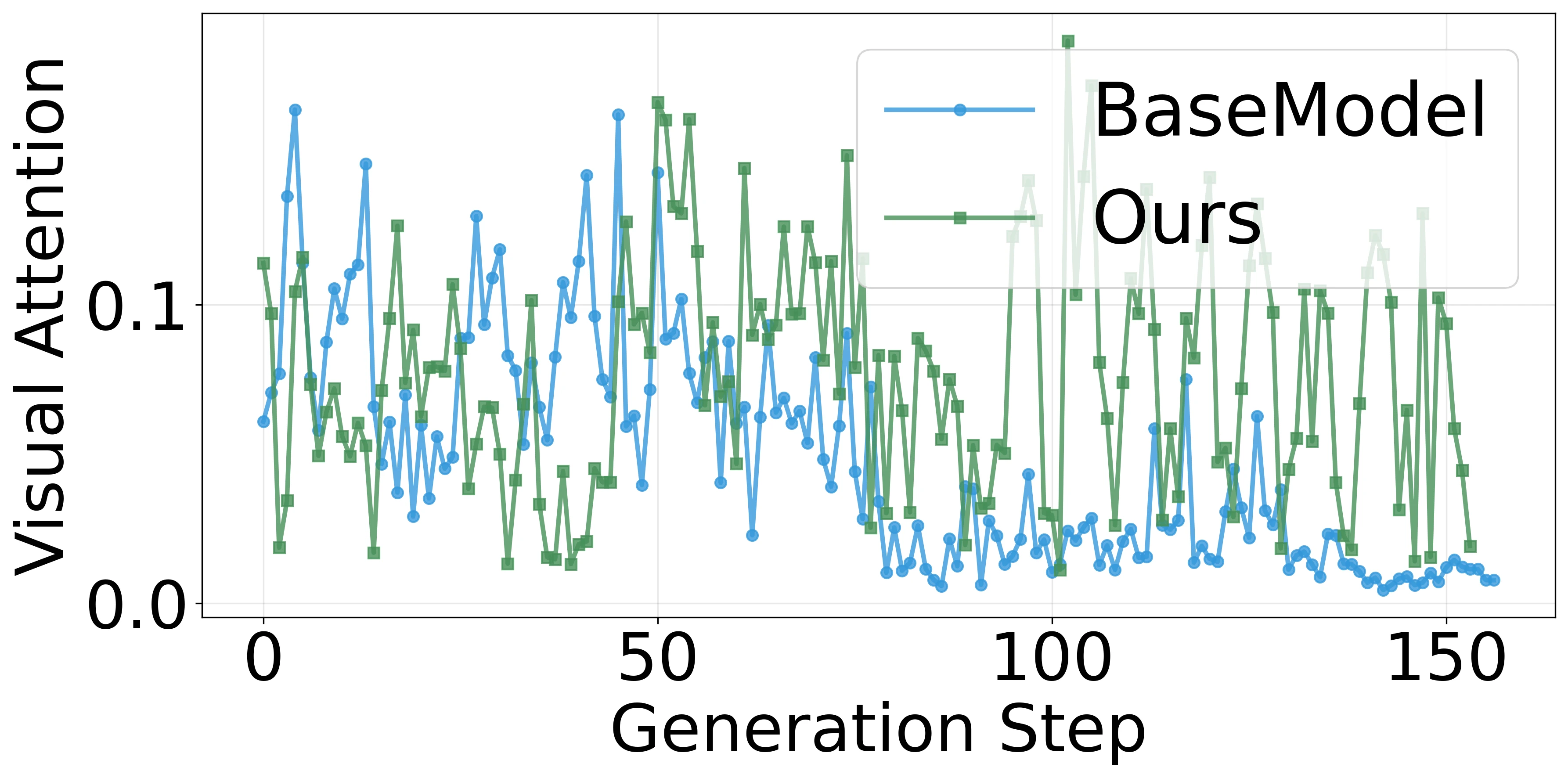
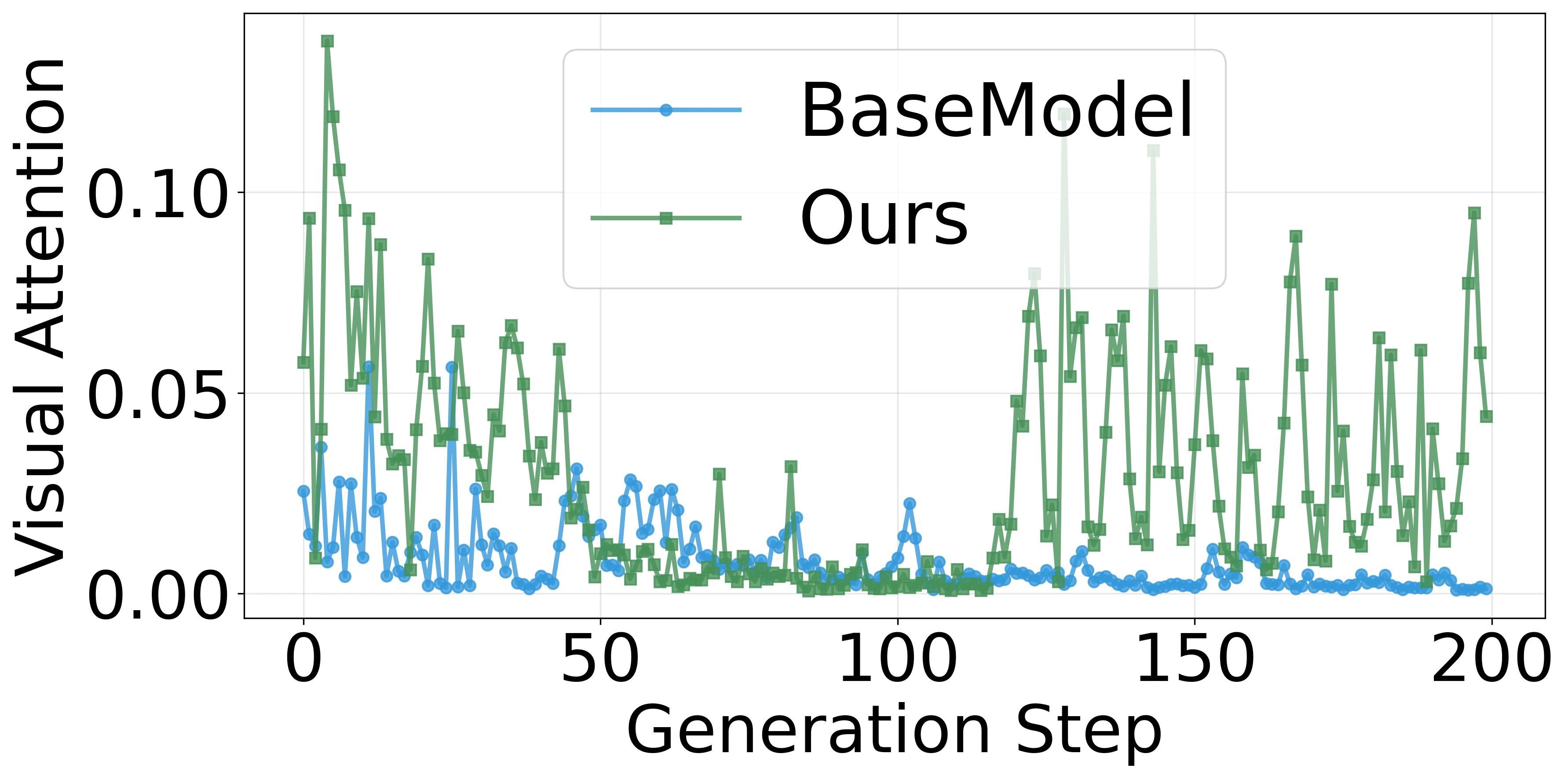
Our auto-encoder uses a rendering engine as decoder that reconstructs diagrams from symbolic logic forms. This enables self-supervised training through perceptual loss between input diagrams and their reconstructions. To address training collapse due to sparse supervision, we introduce two stabilization strategies:

Hard Negative Contrastive Learning: Gaussian noise injection to increase reward variance.
Power Normalization Annealing: Amplifies reward differences while preserving relative ranking.

Main Results

We evaluate our symbolic auto-encoder (SymVAE) across three tasks: geometric diagram reconstruction, diagram understanding, and mathematical reasoning.

Geometric Diagram Reconstruction

Model	Synthetic Diagrams				Geo170K Diagrams
	MSE↓	LPIPS↓	SSIM↑	DINO↑	MSE↓	LPIPS↓	SSIM↑	DINO↑
Pixel-Level Auto-Encoder
VAE	12.9	0.29	0.62	0.81	37.9	0.37	0.64	0.80
VQ-GAN	11.7	0.21	0.69	0.81	37.2	0.31	0.73	0.83
Close-Source MLLMs
GPT-4o	34.3	0.15	0.82	0.96	39.9	0.22	0.76	0.92
Our Symbolic Models
SymParser-3B	7.64	0.12	0.76	0.93	36.8	0.28	0.76	0.93
SymHPR-3B	7.02	0.08	0.83	0.96	27.7	0.26	0.77	0.95
SymVAE-3B	6.13	0.01	0.89	0.95	21.8	0.20	0.79	0.95
SymVAE-7B	6.01	0.05	0.94	0.96	16.8	0.17	0.83	0.96

Key Findings

Superior Reconstruction Fidelity: SymVAE-7B achieves the best performance across all metrics on both synthetic and real-world diagrams.
Outperforms Closed-Source Models: SymVAE-7B significantly surpasses GPT-4o on MSE (6.01 vs 34.3 on synthetic; 16.8 vs 39.9 on Geo170K).

Diagram Understanding

We evaluate on the MathGlance benchmark covering plane geometry, solid geometry, and graphs.

Model	Size	Avg.	Plane Geo.	Solid Geo.	Graphs
GPT-4o	-	53.3	42.8	60.7	56.4
GPT-o4-mini-high	-	48.0	19.1	64.7	60.1
Qwen2.5-VL	7B	59.2	44.0	63.1	65.7
Math-LLaVA	13B	40.0	27.9	44.8	47.3
Primitive	7B	46.6	35.4	49.4	55.1
SymVAE+GeoPeP	7B	72.6	77.9	67.6	72.2

Mathematical Reasoning

MathVerse Results

Model	All	Vision Int.	Vision Only
G-LLaVA-7B	16.6	17.2	9.4
Math-LLaVA-13B	24.1	17.6	16.4
MAVIS-7B	28.4	24.7	18.3
Qwen2.5-VL-7B	49.2	33.2	21.1
SymVAE+CoTs-7B	51.8	35.2	24.9

GeoQA Results

Model	Accuracy (%)
G-LLaVA-7B	64.2
MAVIS-7B	66.7
MultiMath-7B	74.1
Qwen2.5-VL-7B	76.4
SymVAE+CoTs-7B	79.4

Cross-Modal Attention Visualization

Attention on MathGlance — Geometric Description Task

Reconstruction Visualization

Comparison of geometric reconstructions between our approach and general-purpose multimodal models. General-purpose multimodal models struggle to preserve fine-grained geometric structure, whereas our approach yields substantially more faithful geometric and relational reconstructions.

Logic Form Examples

Our symbolic representations consist of compositional geometric primitives organized in a hierarchy: Points → Lines → Shapes → Shape Indicators → Relations.

Cross-Domain Generalization

Our symbolic encoder demonstrates strong cross-domain generalization, extending beyond geometric diagrams to electrical circuits and chemical structures.

Chemical structure reconstruction

Electrical circuit reconstruction

Cross-Lingual and Cross-Modal Transfer

Emergent Cross-Lingual Transfer

After fine-tuning on perception tasks, our model exhibits emergent cross-lingual transfer: formal logic forms are automatically translated into fluent natural-language chain-of-thoughts without any explicit CoT supervision.

Emergent Cross-Modal Adaptation

Although trained only on 2D geometric diagrams, the model automatically adapts point primitives to 3D scenes, enriching them with attributes such as object shape, color, and material.

Qualitative Reasoning Examples

Our model produces correct reasoning chains grounded in accurate visual perception.

BibTeX

@article{zhang2025symhpr,
  title={Hierarchical Process Reward Models are Symbolic Vision Learners},
  author={Zhang, Shan and Chen, Aotian and Zou, Kai and Gu, Jindong and Xue, Yuan and van den Hengel, Anton},
  journal={arXiv preprint arXiv:2512.03126},
  year={2025}
}